Codificación aprenderaprogramar.com: PN00544G
REPRESENTACIÓN GRÁFICA EN EL PLANO CARTESIANO CON DIDAC-PROG CARTESIA
¡Hola a todos! Continuamos con nuestro tutorial de programación para niños a partir de 12 años. En anteriores entregas hemos visto cómo representar una función sobre el plano cartesiano y también cómo representar la función valor absoluto de una dada desde un punto de vista más teórico. Vamos a ver ahora cómo hacer esto programando con nuestro ordenador.

Esta entrega la catalogamos como de programación avanzada. Por tanto no es recomendada para primaria sino sólo para secundaria.
| Esta entrega está dirigida a mayores de 12 años. Si tienes menos edad, sáltala. |
Diversas funciones matemáticas no se incluyeron en la aplicación Didac-Prog Cartesia pensando en mantener la aplicación simple. No obstante, es posible que se incorporen en versiones futuras en función de la valoración pedagógica y la demanda que por parte de los usuarios se perciba.
Entre las funciones no existentes explícitamente en Cartesia tenemos el valor absoluto, logaritmos o funciones trigonométricas entre otras. No obstante parte de las funciones no incluidas pueden simularse utilizando las herramientas de las que disponemos. A esto se le llama sacar partido a la potencia computacional del lenguaje, es decir, hacer cosas no previstas directamente por el lenguaje pero que se pueden hacer a partir de otras cosas más simples.
EL EJEMPLO DE PARTIDA
La función que tomamos como ejemplo es y = x2 – 5 En la anterior entrega vimos cómo obtener puntos y que uniéndolos obteníamos la gráfica de la parábola, que es así:
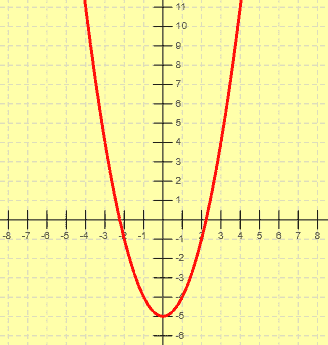
También hicimos lo mismo con la función valor absoluto de la parábola y = | x2 – 5 |
Vamos a ver ahora cómo podemos crear un programa que represente esta función valor absoluto.
El valor absoluto es fácilmente simulable en Didac-Prog Cartesia usando el condicional, y de eso nos vamos a valer para crear nuestro programa.
REPRESENTAR LA FUNCIÓN VALOR ABSOLUTO DE OTRA FUNCIÓN
A continuación se muestra un programa que sirve de ejemplo de cómo representar la función valor absoluto de la misma parábola utilizada anteriormente. Ejecútalo en tu computador y comprueba el resultado.
|
--PROGRAMA VALOR ABSOLUTO PN00544G-1: APROXIMA EL DIBUJO DE VALOR ABSOLUTO DE UNA PARÁBOLA A BASE DE SEGMENTOS -- Parábola y = x^2-5 Iniciar programa Nuevo grosor lápiz (2) Nuevo color lápiz (1) x nuevo valor es (-6) -- x del punto actual y nuevo valor es (x^2-5) -- y del punto actual a nuevo valor es ((x+0.25)^2-5) -- y siguiente punto
Repetir (64) veces ejecutar bloque Comienzo bloque
Si verdadero (y<0) ejecutar bloque -- Si es negativo tomaremos positivo Comienzo bloque y nuevo valor es (-y) -- valor absoluto, tomamos el opuesto Fin bloque
Si verdadero (a<0) ejecutar bloque -- Si es negativo tomaremos positivo Comienzo bloque a nuevo valor es (-a) -- valor absoluto, tomamos el opuesto Fin bloque
Dibujar línea desde (x,y) hasta (x+0.25, a) x nuevo valor es (x+0.25) -- nueva x actual y nuevo valor es (x^2-5) -- nueva y actual a nuevo valor es ((x+0.25)^2-5) -- y del punto siguiente
Fin bloque
Finalizar programa
|
El resultado que se obtiene es similar a esto:

¿Qué técnica hemos usado para representar esta parábola? Hemos usado una técnica ya comentada anteriormente: tomamos dos puntos cuyos valores x son x y x+0.25 (el valor 0.25 es una pequeña distancia de separación que hemos tomado así a conveniencia, podríamos haber tomado otro valor) y dibujamos un segmento entre los puntos (x, x^2-5) y el siguiente punto que es (x+0.25, (x+0.25)^2 – 5). Uniendo segmentos rectos muy pequeñitos vamos dibujando la forma de la curva.
Para aplicar el valor absoluto, determinamos si la coordenada y de alguno de los dos puntos que utilizamos es menor que cero, y en caso de ser menor que cero tomamos su opuesto, es decir, le quitamos el signo negativo. Por ejemplo si para el punto (x, y) la y vale -4 tomamos – (-4) que es +4. Esto lo hacemos en este fragmento de código:
|
Si verdadero (y<0) ejecutar bloque -- Si es negativo tomaremos positivo Comienzo bloque y nuevo valor es (-y) -- valor absoluto, tomamos el opuesto Fin bloque |
Lo mismo hacemos con el siguiente punto que hemos representado como (x+0.25, a)
Si la y ó la a vale 3, como ya es positivo no tenemos que hacer ningún cambio.
Fíjate que en el panel de mensajes se nos indica que se han usado coordenadas fuera del área visible. ¿Por qué? Por los valores que hemos tomado para representar. Nosotros hemos puesto que se comience con un valor de x igual a menos 6, y para este valor la y que se obtiene es 36-5 = 31, es decir, el punto a representar sería (-6, 31). Sin embargo, nuestro panel de dibujo no es tan grande como para poder representar ese punto (la máxima coordenada y es 10 aproximadamente) por lo que se nos muestra el aviso.
Comenzando en -6, en cada repetición avanzamos 0.25 unidades, con lo cual cuando llegamos a aproximadamente (-4, 11) comienza a hacerse visible el trazado en la pantalla.
RESUMEN
Hemos llegado al final de esta entrega del curso. A modo de resumen, hemos visto que podemos crear funciones que no están disponibles directamente en Didac-Prog Cartesia a través del uso de las herramientas del lenguaje de las que disponemos como condicionales y bucles. El único límite que tienes a la hora de plantear programas es tu creatividad e imaginación. ¡Nos vemos en la próxima entrega!
EJERCICIO
Crea un programa de Didac-Prog Cartesia donde uses una única variable, la variable x, para establecer el valor de las x. Los puntos debes expresarlos usando la variable x. Vete ampliando el programa para cumplir lo que se va pidiendo en cada apartado:
a) Dibuja la recta y = 2*x – 3 sin usar bucles. La recta debe dibujarse en color rojo y trazo grueso. Pista: usa dos puntos lejanos (los puedes obtener por ejemplo con x= – 11 para el primer punto y sumarle 30 uds a la x para el segundo punto).
b) Determina en qué punto el valor de y empieza a ser negativo. Para ello mira el dibujo y determina el punto según el dibujo. Luego, ten en cuenta que el valor exacto se obtiene haciendo y = 0, es decir, 0 = 2*x – 3 y de ahí obtenemos x = 3 / 2 teniendo en cuenta que 3/2 = 1.50 resulta el punto (3/2, 0) Responde: ¿Coincide aproximadamente con el punto que habías determinado observando el dibujo? ¿Los valores de la coordenada y se hacen negativos hacia la izquierda o hacia la derecha de x = 3 / 2? Por ejemplo, calcula los valores de y para los valores de x “hacia la derecha” 2, 3, 4, y 5 así como para los valores de x “hacia la izquierda” 1, 0, -1, -2. Si queremos representar el valor absoluto de la función, ¿en qué casos tendríamos que aplicar un signo menos a la función para obtener un valor positivo, a los valores de la x “hacia la izquierda” o a los valores de x “hacia la derecha”?
c) En el mismo programa anterior, dibuja la función valor absoluto y = | 2*x – 3| sin usar bucles y usando un trazo azul fino. Para ello te bastará cambiar el color de dibujo a azul y el grosor a fino, y establecer el valor de x como 3/2. Después dibuja una recta desde (x, 2*x – 3) hacia un punto lejano a la derecha como (x+30, 2*(x+30) – 3) ya que es positivo y no hay que cambiar el signo, y luego dibuja otra recta desde (x, 2*x – 3) hacia un punto lejano a la izquierda como ( x – 30 , – (2* (x–30) – 3)) ya que al resultar el valor de y negativo hemos de aplicarle el signo menos para obtener el valor absoluto.
d) Observa el trazado de la función original y de la función valor absoluto sobre el gráfico. ¿Qué valor de y se obtiene para x=0 con la función original? ¿Y con la función valor absoluto?
El resultado gráfico a obtener debe ser parecido a esto:
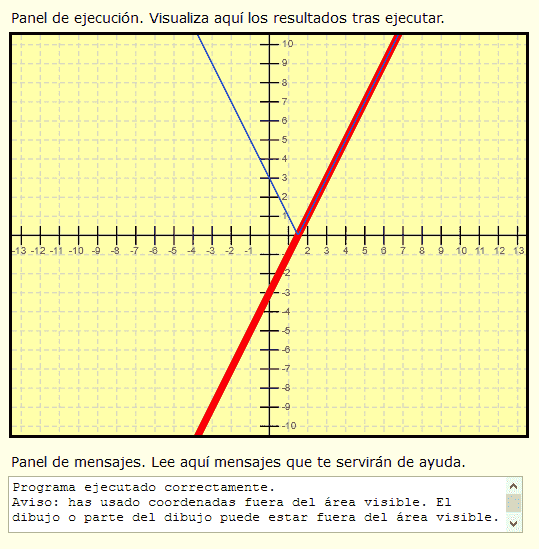
Puedes comprobar si tus respuestas son correctas consultando en los foros aprenderaprogramar.com.
Para acceder a la información general sobre este curso y al listado completo de entregas pulsa en este link: Ver curso completo.
Para hacer un comentario o consulta utiliza los foros aprenderaprogramar.com, abiertos a cualquier persona independientemente de su nivel de conocimiento.


